Insieme funzionalmente completo

Home → Tutorial → Appunti scolastici → Digitale → Insieme funzionalmente completo

stesura preliminare

Non tutte le porte logiche descritte in questa pagina sono necessarie!

Un sotto-insieme di porte che permettono di realizzare una qualunque funzione è detto insieme funzionalmente completo.

AND, OR ed inverter

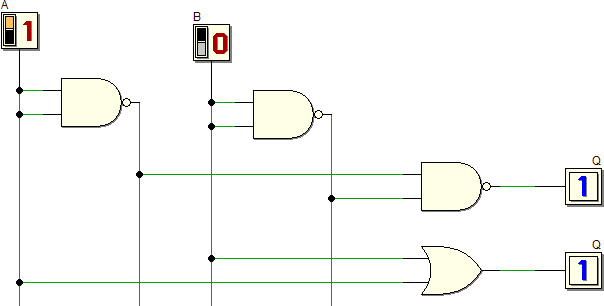
Si può dimostrare che qualunque funziona logica è realizzabile utilizzando esclusivamente porte AND, OR ed inverter che quindi costituiscono nel loro insieme un insieme funzionalmente completo. Per esempio una porta XOR eventualmente presente in un circuito logico può essere sostituita da porte AND, OR ed inverter opportunamente collegati:

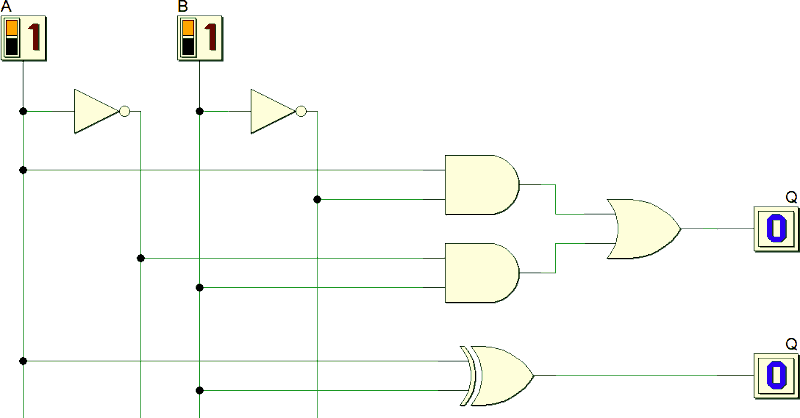
Quando si utilizza il metodo delle le forme canoniche o delle K-map questo assunto è scontato...

AND ed inverter

Un altro insieme funzionalmente completo è costituito dalle sole porte AND e da inverter: è infatti sufficiente sostituire le porte OR eventualmente presenti applicando il teorema di De Morgan ( A + B = A · B):

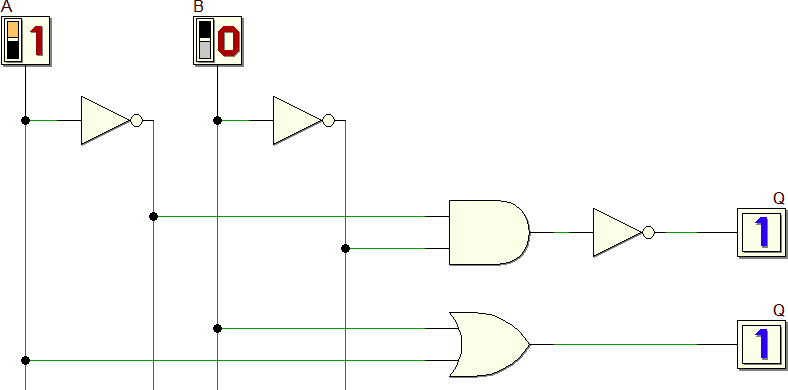
Porta OR realizzata con AND e NOT

Analogamente è possibile realizzare qualunque funzione logica usando esclusivamente porte OR ed inverter.

NAND

La porta NAND costituisce da sola un insieme funzionalmente completo; la porta NAND è detta anche blocco logico universale. Infatti con essa è possibile realizzare circuiti equivalenti a:

inverter, di seguito sono mostrate due possibili soluzioni

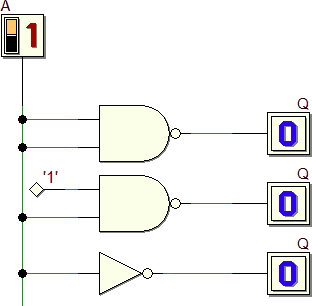
Inverter realizzato con porta NAND

porte AND

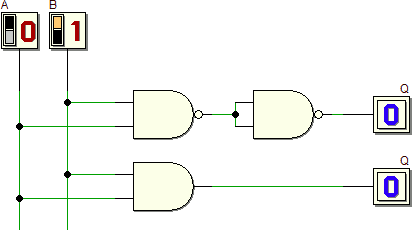
AND realizzato con sole porte NAND

porte OR

OR realizzato con sole porte NAND

[ Attività ] disegnare un circuito equivalente ad una porta XOR usando solo porte NAND

Una particolarità utile a livello applicativo è la possibilità di realizzare una rete SP (somma di prodotti), ottenuta per esempio con la prima forma canonica oppure raccogliendo gli "1" con le K-map, semplicemente sostituendo tutte le porte presenti con porte NAND:

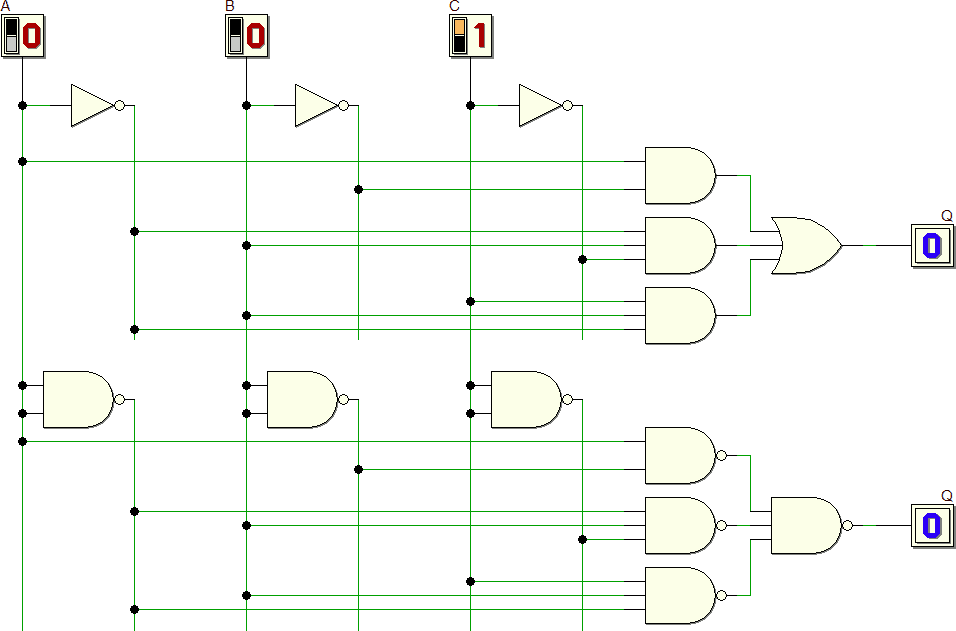
Prim forma canonica con porte NAND

La "dimostrazione" intuitiva può essere fatta sostituendo le singole porte della rete originale con porte NAND, come sopra mostrato, ed eliminando le doppie negazioni.

NOR

Analogamente è possibile realizzare qualunque funzione logica usando esclusivamente porte NOR.

[ Attività ] Realizzare inverter, porte AND e porte OR utilizzando esclusivamente porte NOR

Anche con le porte NOT è possibile rimpiazzare velocemente tutte le porte presenti in una rete PS (prodotto di somme), ottenuta per esempio con la seconda forma canonica, analogamente a quando mostrato per le porte NAND.

Data di creazione di questa pagina: febbraio 2025
Ultima modifica: 14 febbraio 2025