

Una linea di trasmissione è costituita da due conduttori metallici che hanno lo scopo di trasferire un segnale dal trasmettitore al ricevitore. Sono caratterizzate da una lunghezza significativa: il tempo necessario ad un segnale elettrico per percorrerla non è quindi trascurabile.
Fisicamente una linea di trasmissione può essere un cavo coassiale, tipicamente oggi usato per collegare antenne, oppure un doppino intrecciato (twisted pair), tipicamente usato per la trasmissione di dati digitali a distanze relativamente brevi.


In alcuni casi il filo tra ricevitore e trasmettitore può essere considerato un semplice collegamento diretto: le sue caratteristiche elettriche non hanno alcuna rilevanza ai fini del funzionamento del circuito. Esempi tipici sono i circuiti digitali realizzati con una breadboard o il collegamento di sensori ad Arduino.
In altri casi (collegamenti veloci e/o a distanza) occorre scegliere ed utilizzare con attenzione il cavo, pena il mancato funzionamento del circuito; inoltre le equazioni che regolano tensioni e correnti (equazioni del telegrafista) sono estremamente complesse ed addirittura impossibili da risolvere nel caso generale. In questi casi si parla di linea di trasmissione.
La valutazione preliminare della necessità di usare i concetti presentati in questa pagina aiuta quindi a non complicarsi la vita quando non è necessario... Una regola empirica (rule of thumb) valida in prima approssimazione per un sistema digitale: non è necessario considerare un collegamento come linea di trasmissione se la durata del bit è almeno dieci maggiore del tempo necessario al segnale elettrico per percorrere l'intera linea (nota 7).
Tre esempi:
Le caratteristiche di una linea di trasmissione sono identificate da tre parametri:
La velocità di propagazione v è un concetto semplice:
La velocità di propagazione dipende dal tipo di linea e dalla frequenza del segnale. Per esempio un doppino AWG22 con isolamento in polietilene (PE) ha la velocità di propagazione riportata nel grafico seguente:
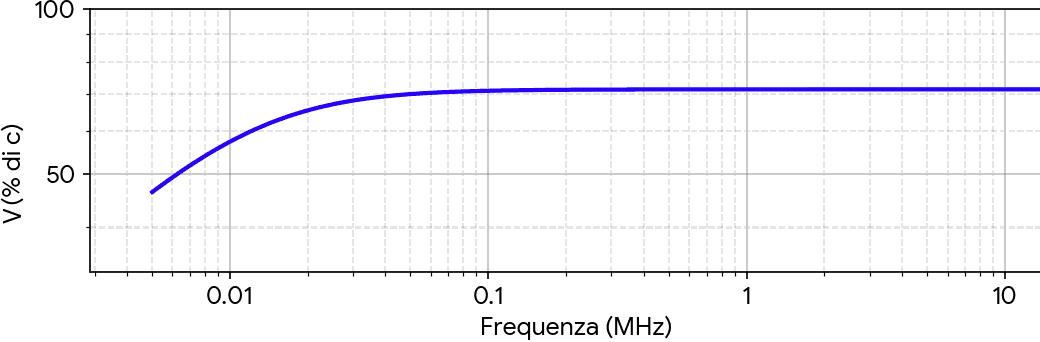
L'andamento di v è tipico di tutte le linee di trasmissione:
Una linea di trasmissione non causa distorsioni se la velocità di propagazione non dipende dalla frequenza. Questo è praticamente sempre verificato a condizione che il segnale trasmetto abbia un frequenza abbastanza elevata.
Il concetto di impedenza caratteristica Z0 non è per nulla intuitivo...
Definizione: Z0 è il rapporto tra la tensione tra i due conduttori e la corrente che scorre; si misura in Ω,
Alcune osservazione:
In realtà l'impedenza caratteristica non è costante, ma dipende dalla frequenza del segnale; essa tende a crescere alle frequenze più basse. Il grafico seguente è, per esempio, relativo ad un doppino AWG22 simile a questo:

Dal grafico di vede che, se f > 20 kHz, Z0 = 100 Ω, valore spesso indicato sui foglio tecnici come impedenza caratteristica di questo doppino.
Una linea di trasmissione non causa distorsioni se:
Le ultime due caratteristiche sono sinteticamente descritta dicendo che la linea è adattata oppure terminata.
La potenza in uscita ad una linea di trasmissione è più piccola della potenza di ingresso. Tale attenuazione (α) viene indicata in decibel ogni 100 m oppure, in quella parte del mondo ancora legato alle obsolete misure imperiali, in decibel ogni 100 piedi.
Formalmente l'attenuazione (di tensione o di potenza) è definita come:
αV = Vin / Vout
αP = Pin / Pout
Oppure, in unità logaritmiche (nota 5):
αdB = VindBV - VoutdBV
αdB = PindBm - PoutdBm
Il grafico seguente è relativo ad un doppino AWG22 e mostra l'attenuazione di 100 m di cavo in funzione della frequenza del segnale sinusoidale:
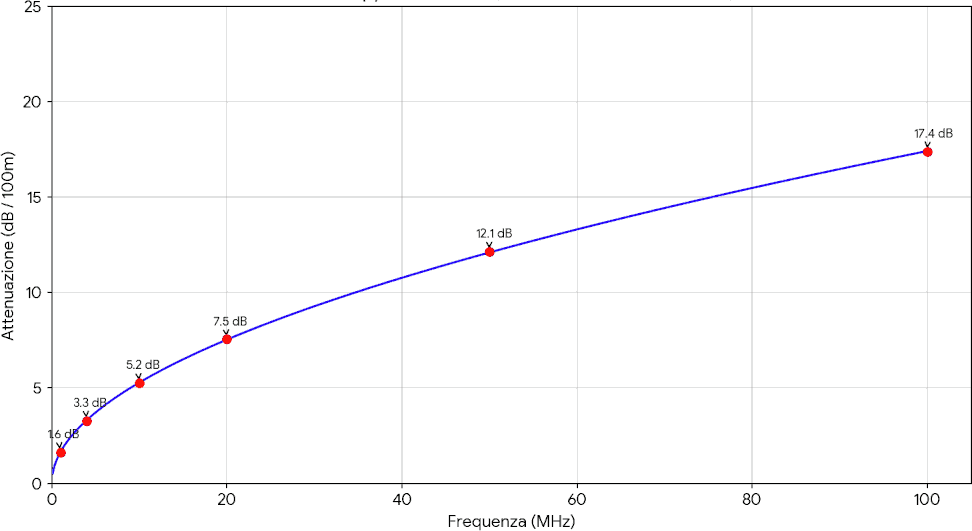
L'attenuazione di 100 m di cavo (o altra lunghezza di riferimento, per esempio 1 km oppure 1 m) a volte è indicata come attenuazione specifica.
Questo grafico è fondamentale per valutare la potenza del segnale di uscita ad un cavo, usando la seguente formula. dall'ovvio significato:
Pout = Pin - αl·l
Dove:
Normalmente una linea di trasmissione è terminata con due connettori, uno per parte, al fine di permettere di collegare e scollegare facilmente le apparecchiature. Questi connettori introducono un'attenuazione supplementare, da sommare a quella propria della linea. L'attenuazione dei connettori dipende dalla loro qualità, ma anche del corretto montaggio, dall'ossidazione (per questo sono normalmente rivestiti in oro), dall'invecchiamento degli isolanti.
Pout = Pin - ( αl·l + 2·αc)
Dove αc è l'attenuazione introdotta da un connettore.
Questa formula è un caso particolare di quella generale nel caso di assenza di amplificatori.
Una linea di trasmissione non causa distorsioni se l'attenuazione è costante, cosa non possibile. Il problema viene affrontato cercando di mantenere l'attenuazione bassa ed utilizzando equalizzatori sia in trasmissione che in ricezione.
Con costanti primarie si fa riferimento alle caratteristiche fisiche ed elettriche di una linea.
Si tratta di un'analisi di una certa complessità, non necessaria per il semplice utilizzo di una linea di trasmissione.
Il primo modello, molto poco accurato, descrive una linea di trasmissione con sei componenti. Un esempio è il seguente:
All'ingresso della linea è presente un generatore di impulsi con resistenza pari nell'esempio a 50 Ω; in uscita è presente un carico costituito da R2, anch'essa da 50 Ω. Il valore di R1 ed R2 deve essere uguale e scelto opportunamente, in base al tipo di linea in uso.
Tale modello viene chiamato a parametri concentrati perché "concentra" in un solo componente puntiforme (L, C, R) proprietà che nella realtà sono "distribuite" per l'intera lunghezza della linea. Questo fatto non mette in evidenza una delle caratteristiche più significative delle linee di trasmissione: il segnale elettrico impiega un tempo significativo per percorrere lo spazio tra ingresso ed uscita.
Un secondo modello descrive una linea di trasmissione come costituita da molti blocchi come quello appena descritto collegati tra di loro in cascata. Per esempio è possibile descrivere una linea di trasmissione lunga 10 m come composta da 10 blocchi, ciascuno lungo un metro:

La risposta all'impulso è mostrata nel grafico seguente, dove in verde è rappresentato l'ingresso ed in rosso l'uscita:

Pur essendo i segnali piuttosto distorti, si nota uno degli aspetti fondamentali: il segnale in uscita arriva dopo quello di ingresso, circa 50 ns in figura. La cosa è piuttosto ovvia se si considera che un segnale elettromagnetico lungo una linea di trasmissione si propaga a circa 2/3 della velocità della luce (cioè circa 2·108 m/s, nota 6) o poco più.
vengono indicati come costanti primarie della linea di trasmissione e sono forniti dal costruttore della linea di trasmissione.
Una linea di trasmissione per essere priva di distorsioni richiede che:
La prima di queste condizioni è garantita dal costruttore della linea di trasmissione; la seconda deve essere garantita dall'utilizzatore.
Le costanti primarie derivano da:
Il modello a parametri distribuiti deriva dal precedente considerando una linea costituita da infiniti elementi come quelli già descritti, ciascuno di lunghezza infinitesima.

La risposta all'impulso è simile (nota 2) al comportamento reale:

Si possono osservare:
Con linee più lunghe o segnali più veloci, come logico aspettarsi, questi aspetti divengono più evidenti.
Questo modello di linea deriva dal precedente ignorando i due resistori. In genere vengono forniti due sole costanti, dette costanti secondarie, derivate dalle costanti primarie:

Linee di trasmissione: esercizi
Pagina creata nel gennaio 2021
Ultima modifica: 10 febbraio 2026
Appunti scolastici - Versione 0.1032 - Maggio 2025
Copyright 2012-2025, Vincenzo Villa (https://www.vincenzov.net)
Creative Commons | Attribution-ShareAlike 4.0 International (CC BY-SA 4.0)