
Il segnale sinusoidale assume un'importanza fondamentale in molti aspetti dell'analisi dei segnali elettrici variabili. Tale segnale è caratterizzato nel tempo da un andamento simile alla funzione seno, da cui il nome.
In questa pagina verranno mostrati alcuni modi per descrivere questo segnale; verranno usate soprattutto rappresentazioni grafiche perché più utili in ambito applicativo e perché mascherano aspetti matematici anche molto avanzati, quali i numeri complessi o le serie di Fourier, in genere affrontati nei corsi di matematica solo in anni successivi (o non affrontati affatto nelle scuole superiori...).
Un segnale sinusoidale ha diverse rappresentazioni grafiche:
Nessuna rappresentazione grafica del segnale sinusoidale è perfetta:
Diversi i motivi dell'importanza del segnale sinusoidale:



L'ultimo aspetto è quello concettualmente più importante nel contesto in cui queste pagine sono state scritte.
Un segnale sinusoidale può essere descritto descritto nel tempo da una funzione simile a y(x) = sin(x) (nota 10). La variabile indipendente x è costituita dal tempo, sempre indicato con la lettera minuscola t (normalmente moltiplicato per una costante); la variabile dipendente y è costituita da una tensione oppure da una corrente, anch'esse indicate con lettere minuscole, tipicamente v oppure i.
Come esempio consideriamo un segnale sinusoidale (nota 1) con:
La sua rappresentazione grafica (nel dominio del tempo) è la seguente;

Alcune precisazioni:
In ambito tecnico si preferisce fare riferimento a tensione efficace VRMS, espressa in volt, e frequenza, espressa in hertz.
La sua funzione analitica (nota 1) è la seguente:

Disegnare il grafico di una tensione sinusoidale con ampiezza efficace VRMS = 5 V, frequenza f = 10 kHz. Scrivere inoltre (nota 1) la funzione corrispondente.
Il segnale è sinusoidale e quindi dalla tensione efficace possiamo immediatamente ricavare che la tensione massima è circa VMAX = 7 V e la tensione minima circa Vmin = -7 V.
Il periodo è T = 1/f = 0,1 ms = 100 µs. Il grafico è il seguente:

La pulsazione è ω = 2·π·f = 6,28·104 rad/s. La funzione che descrive tale curva è quindi:
v(t) = 7 · sin(6,28·104 · t)
La rappresentazione di una sinusoide nel dominio del tempo è un'astrazione matematica che:
Per questo è stata introdotta una rappresentazione grafica della sinusoide più semplice da disegnare ed immediata da comprendere: un grafico nel dominio della frequenza:
Tale grafico è spesso chiamato spettro del segnale (nota 7) e la linea verticale linea spettrale.
Come ampiezza può indifferentemente essere scelta la tensione di picco oppure la tensione efficace oppure usare unità logaritmiche come il dBV; per evitare incomprensioni occorre specificare chiaramente quale tensione è stata indicata. È anche possibile utilizzare la potenza, in unità lineari (W) oppure logaritmiche (dB).
Si noti come la rappresentazione grafica nel dominio della frequenza non ha apparentemente nulla in comune con quella nel dominio del tempo.
Una sinusoide con ampiezza di picco 1 V e frequenza 2 kHz può essere disegnata nel dominio della frequenza con il seguente grafico:

Come alternativa, lo spettro della stessa sinusoide può essere rappresentata con il valore efficace, pari in questo caso a circa VRMS = 0,7 V):

Importante: i due grafici precedenti sono diversi, ma rappresentano la stessa sinusoide! Occorre sempre specificare se la tensione rappresentata nel grafico è quella di picco oppure quella efficace.
Due sinusoidi possono differire tra di loro, oltre che per ampiezza e frequenza, anche per il ritardo temporale tra di esse, misurato in corrispondenza del passaggio per l'asse orizzontale. In particolare siamo interessati ad esaminare il caso in cui le due sinusoidi hanno la stessa frequenza.

Il ritardo TD può essere espresso:
T : 360° = TD : φ (nota 9)
T : 2π = TD : φ (nota 9)
La lettera greca φ è chiamata fase tra i due segnali ed è espressa in gradi oppure in radianti (nota 6).
Due sinusoidi in ritardo tra di loro sono dette sfasate (cioè con fase diversa da zero).
Il grafico seguente mostra due sinusoidi con la stessa frequenza (f = 1/2 µs = 500 kHz) ed ampiezza di picco diversa (3 V e 2 V).

Il segnale verde è in ritardo di 167 ns rispetto a quello rosso; in alternativa possiamo dire che il segnale rosso è in anticipo di 167 ns rispetto a quello verde.
Partendo dalla relazione T : 360° = TD : φ possiamo calcolare la fase come φ = 167/2000·360 = 30°.
Partendo dalla relazione T : 2π = TD : φ possiamo calcolare la fase come φ = 167/2000·6,28 = 0,5 rad.
Possiamo indicare la fase anche per una singola sinusoide, espressa rispetto ad una "sinusoide immaginaria" passante per l'origine degli assi ed utilizzando le stesse relazioni sopra riportata. Si tratta di un artificio matematico in quanto, dal punto di vista fisico, l'istante t = 0, e quindi la posizione dell'asse verticale, è arbitrario.
Per quanto riguarda il segno, la fase è positiva se la sinusoide è in anticipo (cioè "inizia prima" dell'asse verticale), negativa per le sinusoidi in ritardo ("inizia dopo" dell'asse verticale).
Possiamo inserire la fase (espressa in radianti) nella funzione analitica del segnale sinusoidale:

Nell'esempio seguente abbiamo una sinusoide, non passante per l'origine degli assi.

Osservare con attenzione la posizione dell'asse verticale (t = 0): non è disegnato all'estrema sinistra del grafico.
Per individuare il segno positivo o negativo della fase possiamo:
La funzione corrispondente è:

Per una verifica dei risultati si può calcolare la funzione per t = 0 (o altri punti) e confrontare con il grafico:
v(0 s) = 2 · sin (π/4) = 1.41 V
v(1 µs) = 2 · sin (π + π/4) = -1.41 V
Una rappresentazione vettoriale (o nel piano complesso) mette in evidenza la fase e l'ampiezza della sinusoide attraverso un vettore (fasore) la cui origine coincide con quella degli assi cartesiani:
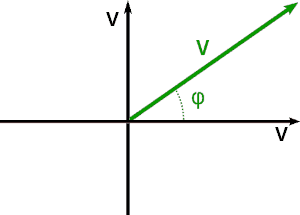
Spesso, invece del vettore, viene semplicemente disegnato un punto in corrispondenza della punta; fase e ampiezza normalmente non sono in questo caso indicati numericamente, ma possono essere facilmente ricavati con righello e goniometro:
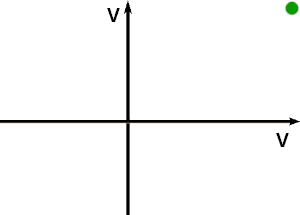
Su entrambi gli assi sono indicate tensioni, ma a volte è tollerato non indicare nulla.
L'immagine seguente mette in relazione il fasore con la sinusoide nel dominio del tempo. In particolare si osservi la linea orizzontale rossa che indica l'istante in cui la sinusoide "inizia" e l'ordinata del fasore.
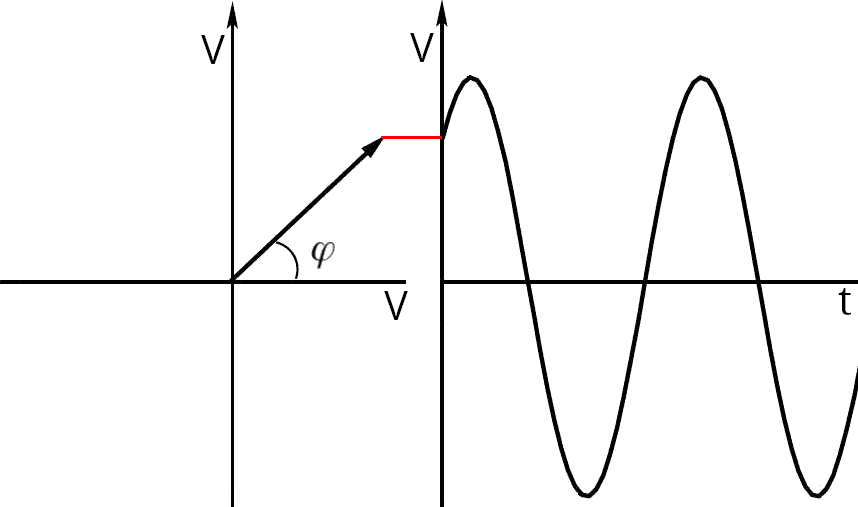
Se |φ| < 90° (come nell'esempio precedente) il tratto iniziale della sinusoide sale: immaginiamo il vettore che con il passare del tempo ruota in senso anti-orario (positivo) e quindi la linea rossa sale ancora.
Se invece φ > 90° il tratto iniziale della sinusoide scende: immaginiamo il vettore che con il passare del tempo ruota in senso anti-orario (positivo) e quindi la linea rossa scende ancora.
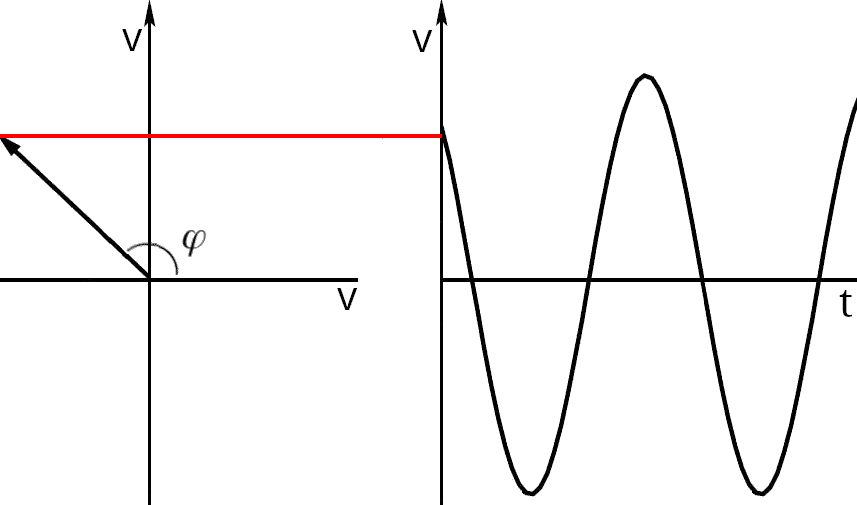
Come ultimo esempio consideriamo una fase compresa tra -90° e 0°(negativa): inizialmente la sinusoide ha valore negativo, ma il tratto iniziale sale: immaginiamo il vettore che con il passare del tempo ruota in senso anti-orario (positivo) e quindi la linea rossa sale.
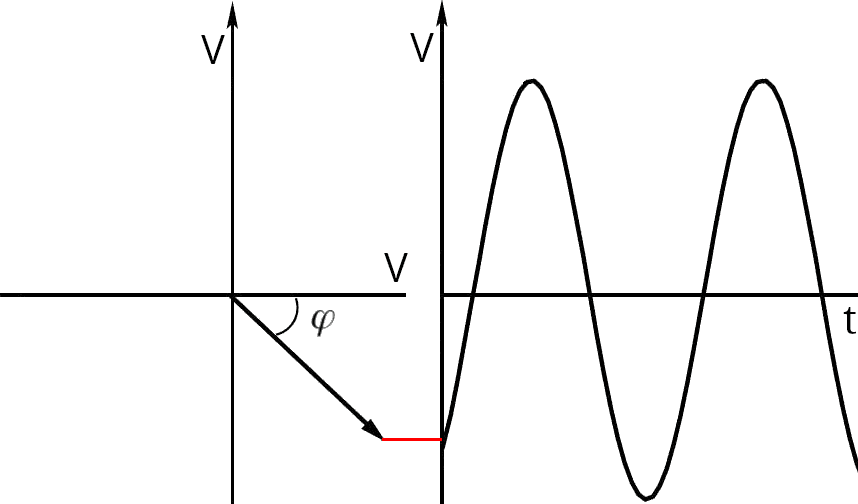
Domanda: come appare il grafico di una sinusoide con fase compresa tra -180° e -90°?
La contropartita di questa rappresentazione è la perdita dell'informazioni relativa alla frequenza, informazione che deve essere fornita separatamente (se necessaria).
Questa rappresentazione è tipica del metodo simbolico che utilizza numeri complessi per rappresentare sinusoidi. Di conseguenza il grafico corrispondente è a volte indicato come piano complesso, l'asse orizzontale come asse reale, quello verticale come asse immaginario.
Il grafico seguente riporta in rosso il fasore che rappresenta una sinusoide con:
In verde una rappresentazione alternativa.
Con questa rappresentazione grafica non abbiamo alcuna informazione sulla frequenza della sinusoide.

Simulacro di Paolina Borghese, ritratta come Venere vincitrice da Antonio Canova nel primo decennio del diciannovesimo secolo - Architas - CC BY-SA 4.0
Data di creazione di questa pagina: aprile 2020
Ultima modifica: 17 dicembre 2025
Appunti scolastici - Versione 0.1032 - Maggio 2025
Copyright 2012-2025, Vincenzo Villa (https://www.vincenzov.net)
Creative Commons | Attribution-ShareAlike 4.0 International (CC BY-SA 4.0)